Misją Instytutu jest dzialalność naukowo-badawcza prowadząca do nowych rozwiązań technicznych i organizacyjnych użytecznych w kształtowaniu warunków pracy zgodnych z zasadami bezpieczeństwa pracy i ergonomii oraz ustalanie podstaw naukowych do właściwego ukierunkowywania polityki społeczno-ekonomicznej państwa w tym zakresie.

Sterowaniem adaptacyjnym nazywa się sterowanie procesu o zmieniających się właściwościach dynamicznych oraz zmieniających się właściwościach zakłóceń stochastycznych, w trakcie którego przeprowadza się estymację parametrów modelu procesu i zakłóceń w celu uaktualnienia parametrów algorytmu sterowania.
Aktywna redukcja hałasu jest procesem na który ma wpływ duża liczba szybkozmiennych czynników zakłócających. Aby skuteczność układu aktywnej redukcji hałasu była odpowiednio duża w zmieniających się warunkach pracy, układ sterujący musi na pojawienie się zakłócenia zareagować w bardzo krótkim czasie. Z tego powodu w układach aktywnej redukcji hałasu szczególnie ważna rola przypada układom adaptacyjnym i efektywnym algorytmom adaptacji. Badania nad adaptacyjnymi układami sterującymi w układach aktywnej redukcji hałasu prowadzone są równolegle w kilku głównych kierunkach. Redukcji hałasu wąskopasmowego i szerokopasmowego, redukcji w przestrzeni otwartej, pomieszczeniach, przy wylotach falowodów itd. Należy podkreślić, że pomimo prowadzonych badań ich obszar jest na tyle rozległy, że wiele kwestii wciąż pozostaje otwartych. Wiele omówionych dalej układów testowano jedynie w warunkach laboratoryjnych do redukcji dźwięków w postaci tonów sinusoidalnych. Najnowsze technologie elektroniczne umożliwiają zbadanie tych układów w warunkach rzeczywistych i na podstawie tych badań wprowadzenie odpowiednich ulepszeń.
I. LMS
Zadaniem takiego algorytmu jest minimalizacja błędu średniokwadratowego związanego z sygnałem e(n). Do szacowania błędu średniokwadratowego można wykorzystać chwilowy kwadrat sygnału błędu czyli:
![]() (w.1)
(w.1)
Estymata gradientu jest równa chwilowemu gradientowi pojedynczej, podniesionej do kwadratu próbki sygnału błędu:
![]() (w.2)
(w.2)
Ponieważ:
![]() (w.3)
(w.3)
estymata gradientu powierzchni błędu średniokwadratowego ma postać:
![]() (w.4)
(w.4)
Wykorzystując powyższe zależności algorytm LMS można przedstawić w postaci:
![]() (w.5)
(w.5)
Powyższa zależność obowiązuje dla filtru o skończonej odpowiedzi impulsowej (SOI). Zasadę działania algorytmu LMS możemy opisać w następujących krokach:
1) ustalamy początkowe wartości parametrów algorytmu adaptacyjnego oraz filtru SOI, którego wagi będą podlegać aktualizacji,.
2) obliczamy wartości próbek sygnału wyjściowego y(n) przez przefiltrowanie sygnału odniesienia x(n) zrealizowane za pomocą operacji:
![]() (w.6)
(w.6)
3) obliczamy sygnał błędu e(n):
![]() (w.7)
(w.7)
4) uaktualniamy wektor wag filtru adaptacyjnego:
![]() (w.8)
(w.8)
Algorytm LMS zbiega w średnim sensie do optymalnego wektora wag wo wtedy i tylko wtedy, gdy:
![]() (w.9)
(w.9)
gdzie: λmax jest największą wartością własną macierzy autokorelacji sygnału odniesienia. Zależność powyższa określająca warunki dla kroku korekcji ze względu na stabilność algorytmu LMS z praktycznego punktu widzenia jest mało użyteczna, gdyż obliczenie wartości λmax dla dużych wartości rzędu filtru L jest bardzo czasochłonne. W zastosowaniach praktycznych stosuje się więc metody szacowania wartości λmax. Przykładowo, jeśli zauważymy, że ślad macierzy R:
![]() (w.10)
(w.10)
to:
![]() (w.11)
(w.11)
gdzie:
![]() (w.12)
(w.12)
jest mocą x(n). Stąd przyjęcie:
![]() (w.13)
(w.13)
zapewnia spełnienie warunku stabilności. Zależność powyższa zapewnia zbieżność średniej wagi. Zbieżność wariancji wagi lub błędu średniokwadratowego wymaga ostrzejszych ograniczeń na krok korekcji μ. Dla sygnałów gaussowskich zbieżność błędu średniokwadratowego wymaga spełnienia warunku:
![]() (w.14)
(w.14)
Odmianą algorytmu najmniejszych średnich kwadratów LMS, w którym wprowadzono modyfikację umożliwiającą zwiększenie szybkości zbiegania bez pogorszenia parametrów pracy w stanie ustalonym jest znormalizowany algorytm LMS zwany algorytmem NLMS. Algorytm NLMS opisany jest zależnością:
![]() (w.15)
(w.15)
w której krok adaptacji obliczany jest za pomocą zależności:
![]() (w.16)
(w.16)
zaś: Px(n) jest estymatą mocy sygnału x(n) w chwili n, podczas gdy α tzw. znormalizowanym krokiem spełniającym warunek:
![]() (w.17)
(w.17)
Wyznaczenie zmiennego kroku korekcji wymaga oszacowania mocy sygnału odniesienia x(n). W spotykanych rozwiązaniach stosuje się dwie metody szacowania: metodę okna prostokątnego i eksponencjalnego. Metoda przesuwanego okna prostokątnego bazuje na zależności:
![]() (w.18)
(w.18)
gdzie: M jest szerokością okna mierzoną liczbą próbek sygnału.
Zaletą tej metody jest dokładność szacowania, natomiast wadą duże wymagania dotyczące pamięci. W przypadku okna eksponencjalnego wymagania pamięci są znacznie mniejsze bowiem szacowanie jest wykonywane na podstawie następującej zależności:
![]() (w.19)
(w.19)
gdzie: β jest współczynnikiem wygładzającym.
Odpowiedni dobór szerokości okna może dodatkowo uprościć obliczenia związane z szacowaniem mocy sygnału odniesienia. Jeżeli szerokość okna M jest równa liczbie współczynników filtru adaptacyjnego L to możemy napisać:
![]() (w.20)
(w.20)
Inną odmianą algorytmu LMS jest korelacyjnym algorytmie LMS. Do wyznaczenia kroku korekcji wykorzystuje się w nim korelację pomiędzy sygnałem odniesienia i sygnału błędu. Podstawą tego podejścia jest fakt, ze w momencie, gdy filtr adaptacyjny jest odstrojony od postaci optymalnej korelacja ρ pomiędzy sygnałami x(n) i e(n) jest duża. W miarę dostrajania filtru, czyli zbiegania algorytmu adaptacyjnego korelacja ρ maleje, by w końcu, gdy wektor współczynników filtru adaptacyjnego przyjmie optymalną postać stać się równą zeru czyli:
![]() (w.21)
(w.21)
W korelacyjnym algorytmie LMS wartość kroku korekcji jest duża na etapie gdy algorytm jest daleki od punktu zbiegnięcia i maleje w miarę zbiegania do bardzo małych wartości, dzięki którym w stanie ustalonym osiągane są bardzo małe wartości odchylenia od minimalnego błędu średniokwadratowego. Przedstawiony proces można zapisać za pomocą następujących zależności:
|
|
|
|
|
(w.22) |
|
|
gdzie: nadkreślone x(n) jest uśrednionym wektorem sygnału odniesienia, α jest współczynnikiem skali, zaś β współczynnikiem wygładzającym umożliwiającym pracę w warunkach niestacjonarnych.
Dzięki wprowadzeniu malejącej w miarę zbiegania algorytmu adaptacyjnego wartości kroku korekcji algorytm ten jest bardzo stabilny. W momencie osiągnięcia stanu ustalonego krok korekcji jest tak mały, że krótkotrwałe zakłócenia nie powodują istotnych zmian parametrów filtru. Co więcej, układ w stanie ustalonym jest odporny na zakłócenia, które nie są skorelowane z sygnałem odniesienia. Czułość algorytmu może być w sposób prosty zmieniana przez odpowiedni dobór współczynnika skali α. Najlepsze wartości α zależą od konkretnego zastosowania.
II. Układ LMS wąskopasmowy z syntezą kształtu fali
Układ aktywnej redukcji bazujący na kontrolerze z syntezą kształtu fali nazywany dalej układem z kontrolerem 1 był jednym z pierwszych cyfrowych systemów aktywnej redukcji. Schemat blokowy systemu przedstawiony jest na Rys. 1.
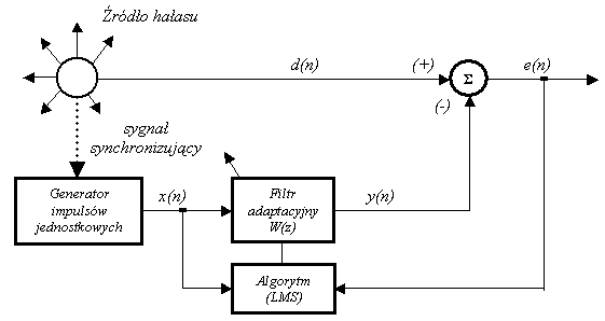
Rys. 1 System aktywnej redukcji z układem syntezy sygnału kompensującego
Generator synchronizowany z okresowym źródłem hałasu (transformatorem) wytwarza ciąg impulsów jednostkowych x(n) opisanych funkcją delty Kroneckera:
![]() (w.1)
(w.1)
Sygnał kompensujący y(n) powstający w wyniku przefiltrowania sygnału x(n) przez filtr adaptacyjny o skończonej odpowiedzi impulsowej rzędu L ma postać:
![]() (w.2)
(w.2)
W układach praktycznych rząd filtru L dobiera się w taki sposób aby był on równy liczbie impulsów N mieszczących się w okresie sygnału odniesienia T0. W takim przypadku zależność (w.2) upraszcza się do postaci:
![]() (w.3)
(w.3)
Wagi współczynników filtru adaptacyjnego aktualizowane są za pomocą algorytmu najmniejszych średnich kwadratów LMS zgodnie z zależnością:
![]() (w.4)
(w.4)
Zależność (w.4) dla sygnału odniesienia (w.1) upraszcza się do postaci:
 (w.5)
(w.5)
Schemat blokowy systemu aktywnej redukcji hałasu transformatora energetycznego z algorytmem syntezy kształtu fali jest przedstawiony na Rys. 2.
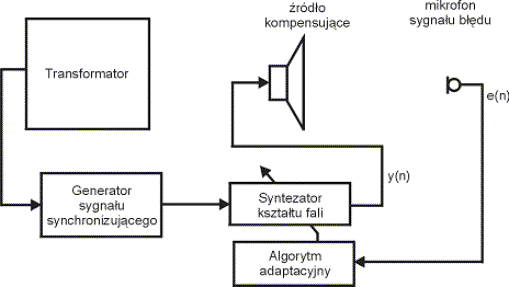
Rys. 2 Schemat blokowy systemu aktywnej redukcji hałasu z algorytmem syntezy kształtu fali
Syntezator kształtu fali jest buforem cyklicznym (kołowym), w którym jednocześnie zapamiętanych jest L próbek sygnału kompensującego. Reprezentują one jeden okres sygnału odniesienia. Generator sygnału synchronizującego pełni rolę zegara, z częstotliwością którego, w sposób sekwencyjny aktualizowane są próbki sygnału w pamięci syntezatora oraz w podobny sekwencyjny sposób próbki sygnału kompensującego (poprzez przetwornik C/A i niezbędne układy pośredniczące dla uproszczenia pominięte na Rys. 2) wykorzystywane do sterowania pracą źródła kompensującego.
Pomiar sygnału błędu e(n) również odbywa się zgodnie z sygnałem generatora synchronizującego. Sygnał błędu jest wykorzystywany do korygowania próbek sygnału kompensowanego. W pierwotnej wersji systemu błąd średniokwadratowy był minimalizowany metodą prób i błędów. Z każdy impulsem generatora sygnału synchronizującego modyfikowana była wartość jednej (i-tej) próbki sygnału w pamięci syntezatora kształtu fali. Jeżeli w wyniku modyfikacji wartość błędu średniokwadratowego zmalała to zmiana wartości próbki była wprowadzana do pamięci syntezatora, w przeciwnym wypadku przywracana była poprzednia wartość próbki. Po przejściu pełnego cyklu prób modyfikacji pozostałych próbek sygnału kompensującego ponownie podejmowana była próba skorygowania i-tej próbki. Podstawowa wadą metody prób i błędów jest wolne i niezależne od wielkości sygnału błędu zbieganie kształtu sygnału kompensującego do postaci optymalnej. Znacznie lepsze wyniki uzyskujemy dzięki wykorzystaniu do korekty próbek sygnału kompensującego, sygnał błędu e(n) czyli zastosujemy podejście analogiczne do korygowania współczynników wag filtru adaptacyjnego w klasycznym szerokopasmowym systemie aktywnej redukcji.
Przed przystąpieniem do właściwych obliczeń opracowano oprogramowanie symulujące pracę rzeczywistego układu synchronizacji kontrolera z sygnałem hałasu wytwarzanego przez transformator. Najważniejsze fazy tworzenia sygnału synchronizującego przedstawione zostały na Rys. 3.

Rys. 3 Kolejne fazy modelowania sygnałów występujących w kontrolerze z syntezą kształtu fali
Na pierwszym (licząc od góry) wykresie przedstawiono sygnał sieci zasilającej (sinusoida o częstotliwości 50Hz). Na drugim wykresie przedstawiono sygnał wytwarzany przez układ pętli synchronizacji fazowej. Jest to sygnał prostokątny zsynchronizowany z sygnałem sieci zasilającej lecz o częstotliwości równej wielokrotności częstotliwości sieci (w tym wypadku zastosowano 4-krotne zwiększenie częstotliwości podstawowej). Na trzecim wykresie przedstawiono sygnał na wyjściu detektora przejścia przez zero, czyli sygnał impulsowy o częstotliwości 8 razy większej od częstotliwości sygnału sieci. Sygnał ten symuluje pracę generatora synchronizującego opisanego zależnością (w.1). Na kolejnym (czwartym) wykresie pokazano przebieg sygnału na wyjściu przetwornika C/A. Zachowano tutaj cechę rzeczywistego przetwornika polegającą na utrzymywaniu stanu wyjściowego w czasie pomiędzy próbkami sygnału synchronizującego. Wykres piąty pokazuje przebieg sygnału błędu w początkowej fazie symulacji (stąd amplituda sygnału błędu jest prawie taka sama jak sygnału odniesienia). Ostatni wykres pokazuje zawartość bufora syntezatora sygnału kompensującego. Jak widać liczba próbek w buforze odpowiada dokładnie współczynnikowi zwielokrotnienia częstotliwości sygnału odniesienia (wykres 1) w sygnale synchronizującym (wykres 3). Widać również, że wartości próbek w buforze „dążą” do kształtu sygnału odniesienia (stąd nazwa typu kontrolera).
III. Układ LMS o strukturze bezpośredniej z generatorem sygnału odniesienia
Schemat blokowy kontrolera przedstawiony został na Rys. 4.

Rys. 4 Schemat blokowy kontrolera z generatorem sygnału odniesienia (struktura bezpośrednia)
Jak widać jest to typowy układ adaptacyjny z filtrem o skończonej odpowiedzi impulsowej. Jedyną różnicą jest zastąpienie mikrofonu pomiarowego generatorem sygnału odniesienia stanowiącym fragment oprogramowania. Ze względu na szczegółowe opisanie tego układu w poprzednich etapach projektu badawczego w niniejszym sprawozdaniu zostało ono pominięte. Generator sygnału sinusoidalnego jest synchronizowany z hałasem transformatora energetycznego w taki sam sposób jak w przypadku przedstawionego w rozdziale IV układ z adaptacyjnymi filtrami wycinającymi.
IV. Układ LMS o strukturze równoległej z filtrami wycinającymi
Podstawową strukturę kontrolera z adaptacyjnym filtrem wycinającym dla sygnału w postaci pojedynczego tonu przedstawiono na Rys. 5.
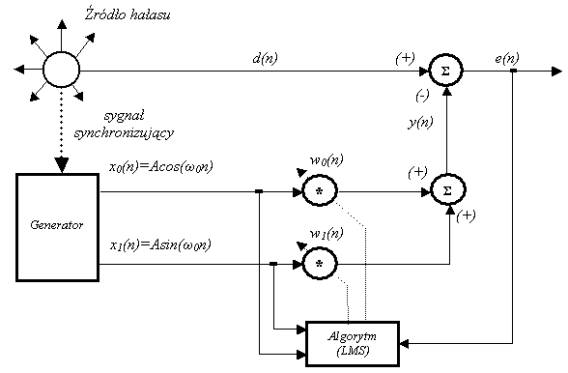
Rys. 5 System aktywnej redukcji hałasu z pojedynczym adaptacyjnym filtrem wycinającym
Zakładamy, że sygnał wzorcowy d(n) ma postać tonu o pulsacji ω0 i przesunięciu fazy φ0:
![]() (w.1)
(w.1)
Generator zsynchronizowany ze źródłem hałasu wąskopasmowego wytwarza sygnał odniesienia składający się z dwóch składników:
![]() (w.2)
(w.2)
Sygnał kompensujący y(n) uzyskiwany jest w wyniku następującej operacji (filtrowania):
![]() (w.3)
(w.3)
Sygnał błędu jest minimalizowany przez zastosowanie algorytmu najmniejszych, średnich kwadratów LMS, który aktualizuje wagi w0 oraz w1 filtru wycinającego zgodnie z zależnościami:
![]() (w.4)
(w.4)
System przedstawiony na Rys. 5 nie uwzględnia wpływu wtórnej ścieżki sygnału. Jej wpływ może być wyeliminowany w analogiczny sposób jak ma to miejsce w przypadku szerokopasmowych systemów aktywnej redukcji hałasu. Na Rys. 6 przedstawiono schemat blokowy systemu aktywnej redukcji hałasu z generacją sygnału odniesienia, w którym transmitancja wtórnej ścieżki sygnału S(z) została uwzględniona w kontrolerze, za pomocą wprowadzenia dodatkowej operacji filtrowania sygnału odniesienia. Mamy tu do czynienia z klasycznym algorytmem FXLMS, w ramach którego wagi filtru aktualizowane są zgodnie z zależnościami:
![]() (w.5)
(w.5)
Sygnały x'0(n) i x'1(n) stanowią przefiltrowane składowe sygnału odniesienia wytworzonego przez generator.

Rys. 6. Schemat blokowy systemu aktywnej redukcji hałasu z filtrem wycinającym i dodatkowymi elementami eliminującymi wpływ wtórnej ścieżki sygnału S(z)
Jeżeli założymy, że transmitancja wtórnej ścieżki sygnału ma postać opóźnienia, możliwe jest uproszczenie struktury z Rys. 6 przez zastąpienie estymat transmitancji S(z) elementami opóźniającymi tak jak to zostało pokazane na Rys. 7. Sygnał kompensujący y(n) obliczany jest zgodnie z zależnością (w.3), zaś uaktualnianie wag filtru adaptacyjnego odbywa się na podstawie zależności:
![]() (w.6)
(w.6)
Wartość opóźnienia Δ może być wyznaczona przed włączeniem systemu aktywnej redukcji hałasu i następnie uwzględniona jako stały parametr kontrolera. Takie podejście jest praktycznie uzasadnione w przypadku, gdy częstotliwość sygnału wzorcowego nie ulega zmianie, bądź zmiany te są niewielkie, tak jak ma to miejsce w przypadku hałasu transformatora. Wynika to z faktu, że opóźnienie Δ zależy od częstotliwości.

Rys. 7 Schemat blokowy systemu aktywnej redukcji hałasu z pojedynczym filtrem wycinającym i opóźnieniami eliminującymi wpływ wtórnej ścieżki sygnału S(z)
Przedstawione wyżej struktury przeznaczone do redukcji hałasu w postaci pojedynczego tonu mogą być przez zrównoleglenie struktur dostosowane do redukcji hałasu, w skład którego wchodzi kilka częstotliwości (składowa podstawowa i harmoniczne). Schemat blokowy kontrolera zastosowany w opracowanym systemie aktywnej redukcji hałasu transformatora przedstawiony jest na Rys. 8.
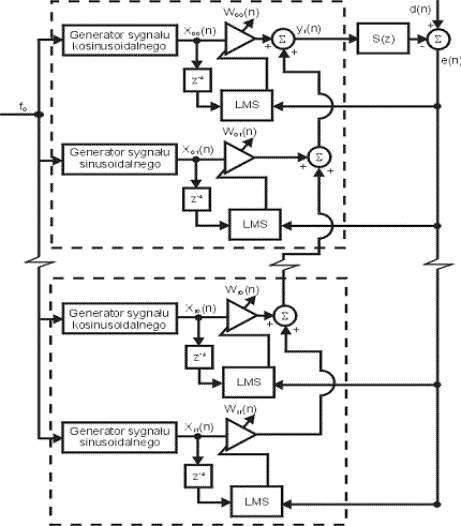
Rys. 8 Schemat blokowy kontrolera z filtrami wycinającymi (struktura równoległa)
Jak widać dla n składowych kontroler zawiera n adaptacyjnych filtrów wycinających. Każdy z tych filtrów przetwarza wewnętrznie wygenerowane sygnały sinusoidalne (kosinusoidalne) o częstotliwościach odpowiadających częstotliwościom składowych eliminowanego hałasu. Sygnały wyjściowe (kompensujące) filtrów podawane są na wspólny węzeł sumacyjny, którego wyjście przeznaczone jest do zasilania źródła wtórnego. Sygnał błędu jest wspólny dla wszystkich filtrów wycinających. Wartości opóźnień eliminujące wpływ wtórnej ścieżki sygnału należy dobrać (zmierzyć) indywidualnie dla każdego filtru (dla każdej składowej sygnału kompensującego).
V. sieci neuronowe
Sztuczne Sieci Neuronowe są szczególnym sposobem realizacji nieliniowego filtra cyfrowego. Powstały one jako pewien model biologicznego układu nerwowego. Podstawowym elementem składowym takiej sieci jest neuron którego model przedstawiono na Rys. 9. Podobnie jak jego biologiczny pierwowzór posiada on N wejść i jedno wyjście. W sieci neuronowej wyjścia poszczególnych neuronów łączą się w odpowiedni, zależny od rodzaju sieci sposób z wejściami innych neuronów.
Sygnał wyjściowy y neuronu stanowi funkcję sumy ważonych sygnałów wejściowych x zgodnie z zależnością:
![]() (w.1)
(w.1)
Gdzie h0 jest wartością progową a hi są wagami poszczególnych wejść. Wielkość wartości progowej może decydować w niektórych przypadkach o przebiegu procesu uczenia sieci. W dalszych rozważaniach jak i badaniach laboratoryjnych przyjęto, że w rozważanych sieciach h0 = 0.

Rys. 6. Model neuronu.
Funkcja F(u) jest nazywana funkcją aktywacji. Najczęściej jako F(u) wykorzystywane są: funkcja jednostkowa, funkcja liniowa, krzywa logistyczna ( funkcja unipolarna) oraz użyty w sieciach neuronowych badanych w omawianym etapie pracy tangens hiperboliczny (funkcja bipolarna). Tangens hiperboliczny opisany jest zależnością:
![]() (w.2)
(w.2)
Na Rys. 10 przedstawiono przebieg funkcji tgh(bu) dla różnych wartości b.
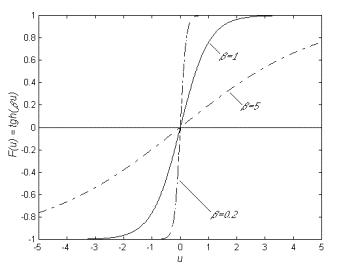
Rys. 10 Funkcja aktywacji tgh(bu) dla różnych wartości b.
Jak już wspomniano istnieje wiele rodzajów sieci neuronowych różniących się sposobem łączenia neuronów. Wśród nich znajduje się przedstawiona schematycznie na Rys. 11 wielowarstwowa sieć jednokierunkowa, która będzie przedmiotem dalszych rozważań. Taką strukturę wybrano z trzech powodów. Po pierwsze sieć tego typu najlepiej sprawdza się w filtracji sygnałów. Sieci neuronowe o innej architekturze są bardziej przydatne do innych zadań, takich jak analiza obrazu, kompresja danych, synteza sygnału mowy. Po drugie algorytm działania tej sieci na sygnałach dyskretnych może być w prosty sposób zaimplementowany w wybranym środowisku programistycznym. Po trzecie sieć taka wraz z jej algorytmem uczenia się może być rozpatrywana jako uogólniony filtr adaptacyjny typu SOI. Dzięki temu możliwe jest zastosowanie (po odpowiedniej adaptacji) do sieci neuronowej niektórych rozwiązań znanych z liniowych filtrów adaptacyjnych.
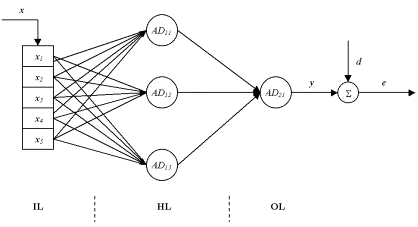
Rys. 11 Wielowarstwowa sieć jednokierunkowa.
Sieć taka składa się z warstwy wejściowej IL, jednej lub więcej warstw ukrytych HL i z warstwy wyjściowej OL. Każdy neuron danej warstwy połączony jest ze wszystkimi neuronami warstwy poprzedniej. Sygnały w sieci płyną tylko w kierunku od wejścia do wyjścia (brak sprzężeń zwrotnych). Działanie przedstawionej na Rys. 9 sieci z jedną warstwą ukrytą i jednym neuronem w warstwie wyjściowej opisane jest zależnościami:
![]() (w.3)
(w.3)
![]() (w.4)
(w.4)
gdzie LX oznacza ilość węzłów w warstwie wejściowej, L ilość neuronów w warstwie ukrytej a podany w nawiasie indeks górny oznacza numer warstwy neuronów począwszy od warstwy ukrytej.
Sygnał wyjściowy sieci y(2) jest w układzie aktywnej redukcji sygnałem kompensującym. Celem uczenia (adaptacji) sieci jest minimalizacja kwadratu błędu (e(2))2 gdzie e(2):
![]() (w.5)
(w.5)
Jednym z najpopularniejszych algorytmów uczenia jest algorytm wstecznej propagacji błędów [12,26,27] Algorytm ten należy do grupy algorytmów gradientowych gdyż korekta wag neuronów sieci następuje w kierunku przeciwnym do znaku składowych wektora gradientu powierzchni błędu e(2). W metodzie tej wagi neuronu w warstwie wyjściowej dla sieci z Rys. 9 będą aktualizowane zgodnie z zależnością:
![]() (w.6)
(w.6)
a wagi neuronów w warstwie ukrytej zgodnie z zależnością:
![]() (w.7)
(w.7)
gdzie
![]() (w.8)
(w.8)
k oznacza numer neuronu w warstwie ukrytej a m jest współczynnikiem uczenia, z reguły dobieranym doświadczalnie z przedziału (0,1). W algorytmie tym błąd z warstwy wyjściowej e(2) propaguje się poprzez wgi neuronów w warstwie wyjściowej do warstwy ukrytej. Stąd nazwa algorytmu.
Jeżeli funkcja aktywacji jest funkcją tgh(bu) to jej pochodna wyraża się wzorem:
![]() (w.9)
(w.9)
Dzięki tej właściwości funkcji tgh(bu) możemy znacznie uprosić obliczenia związane z adaptacją wag sieci neuronowej gdyż wzory (w.6), (w.7) i (w.8) przyjmują wtedy postać:
![]() (w.10)
(w.10)
![]() (w.11)
(w.11)
![]() (w.12)
(w.12)
Należy zauważyć że gdy funkcja aktywacji F(u) jest funkcją liniową to pojedynczy neuron lub warstwa neuronów jest równoważna liniowemu filtrowi SOI, natomiast zależności (w.6) i (w.7) opisują klasyczny algorytm LMS.
Sieć neuronowa z jednym neuronem w warstwie wyjściowej jest przypadkiem szczególnym sieci neuronowej z wieloma neuronami w warstwie wyjściowej. W ogólnym przypadku sygnały wyjściowe sieci neuronowej wyliczane są ze wzoru:
![]() (w.13)
(w.13)
gdzie m jest numerem neuronu w warstwie wyjściowej.
Dla każdego z neuronów warstwy wejściowej sygnał błędu opisany jest zależnością:
![]() (w.14)
(w.14)
W procesie uczenia sieci neuronowej z wieloma wyjściami minimalizowana jest suma kwadratów błędów warstwy wyjściowej. Wagi neuronów warstwy wyjściowej uaktualniane są zgodnie z zależnością:
![]() (w.15)
(w.15)
Proces adaptacji wag neuronów warstwy ukrytej odbywa się nadal zgodnie z zależnością (w.7) jednak ulega zmianie zależność opisująca błąd neuronu tej warstwy. Przyjmuje ona postać:
![]() (w.16)
(w.16)
gdzie M jest liczbą neuronów w warstwie wyjściowej.
© 2002-2004 Centralny Instytut Ochrony Pracy - Państwowy Instytut Badawczy www.anc.pl, www.ciop.pl





